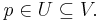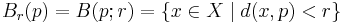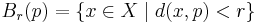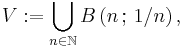Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.
This concept is closely related to the concepts of open set and interior.
Contents |
Definition
If  is a topological space and
is a topological space and  is a point in
is a point in  , a neighbourhood of
, a neighbourhood of  is a subset
is a subset  of
of  , which includes an open set
, which includes an open set  containing
containing  ,
,
This is also equivalent to 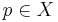 being in the interior of
being in the interior of  .
.
Note that the neighbourhood  need not be an open set itself. If
need not be an open set itself. If  is open it is called an open neighbourhood. Some authors require that neighbourhoods be open, so it is important to note conventions.
is open it is called an open neighbourhood. Some authors require that neighbourhoods be open, so it is important to note conventions.
A set which is a neighbourhood of each of its points is open since it can be expressed as the union of open sets containing each of its points.
The collection of all neighbourhoods of a point is called the neighbourhood system at the point.
If  is a subset of
is a subset of  then a neighbourhood of
then a neighbourhood of  is a set
is a set  which includes an open set
which includes an open set  containing
containing  . It follows that a set
. It follows that a set  is a neighbourhood of
is a neighbourhood of  if and only if it is a neighbourhood of all the points in
if and only if it is a neighbourhood of all the points in  . Furthermore, it follows that
. Furthermore, it follows that  is a neighbourhood of
is a neighbourhood of  iff
iff  is a subset of the interior of
is a subset of the interior of  .
.
In a metric space
In a metric space 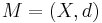 , a set
, a set  is a neighbourhood of a point
is a neighbourhood of a point  if there exists an open ball with centre
if there exists an open ball with centre  and radius
and radius 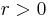 , such that
, such that
is contained in  .
.
 is called uniform neighbourhood of a set
is called uniform neighbourhood of a set  if there exists a positive number
if there exists a positive number  such that for all elements
such that for all elements  of
of  ,
,
is contained in  .
.
For 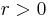 the
the  -neighbourhood
-neighbourhood 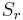 of a set
of a set  is the set of all points in
is the set of all points in  which are at distance less than
which are at distance less than  from
from  (or equivalently,
(or equivalently, 
 is the union of all the open balls of radius
is the union of all the open balls of radius  which are centred at a point in
which are centred at a point in  ).
).
It directly follows that an  -neighbourhood is a uniform neighbourhood, and that a set is a uniform neighbourhood if and only if it contains an
-neighbourhood is a uniform neighbourhood, and that a set is a uniform neighbourhood if and only if it contains an  -neighbourhood for some value of
-neighbourhood for some value of  .
.
Examples
Given the set of real numbers  with the usual Euclidean metric and a subset
with the usual Euclidean metric and a subset  defined as
defined as
then  is a neighbourhood for the set
is a neighbourhood for the set 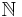 of natural numbers, but is not a uniform neighbourhood of this set.
of natural numbers, but is not a uniform neighbourhood of this set.
Topology from neighbourhoods
The above definition is useful if the notion of open set is already defined. There is an alternative way to define a topology, by first defining the neighbourhood system, and then open sets as those sets containing a neighbourhood of each of their points.
A neighbourhood system on  is the assignment of a filter
is the assignment of a filter 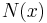 (on the set
(on the set  ) to each
) to each  in
in  , such that
, such that
- the point
 is an element of each
is an element of each  in
in 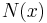
- each
 in
in 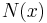 contains some
contains some  in
in 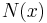 such that for each
such that for each  in
in  ,
,  is in
is in 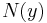 .
.
One can show that both definitions are compatible, i.e. the topology obtained from the neighbourhood system defined using open sets is the original one, and vice versa when starting out from a neighbourhood system.
Uniform neighbourhoods
In a uniform space 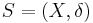 ,
,  is called a uniform neighbourhood of
is called a uniform neighbourhood of  if
if  is not close to
is not close to 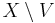 , that is there exists no entourage containing
, that is there exists no entourage containing  and
and 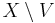 .
.
Punctured neighbourhood
A punctured neighbourhood of a point  (sometimes called a deleted neighbourhood) is a neighbourhood of
(sometimes called a deleted neighbourhood) is a neighbourhood of  , without
, without 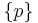 . For instance, the interval
. For instance, the interval 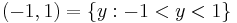 is a neighbourhood of
is a neighbourhood of 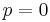 in the real line, so the set
in the real line, so the set 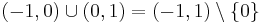 is a punctured neighbourhood of
is a punctured neighbourhood of  . Note that a punctured neighbourhood of a given point is not in fact a neighbourhood of the point. The concept of punctured neighbourhood occurs in the definition of the limit of a function.
. Note that a punctured neighbourhood of a given point is not in fact a neighbourhood of the point. The concept of punctured neighbourhood occurs in the definition of the limit of a function.
See also
References
- Kelley, John L. (1975). General topology. New York: Springer-Verlag. ISBN 0387901256.
- Bredon, Glen E. (1993). Topology and geometry. New York: Springer-Verlag. ISBN 0387979263.
- Kaplansky, Irving (2001). Set Theory and Metric Spaces. American Mathematical Society. ISBN 0821826948.